Regular PolygonsPerimeter of Regular Polygons
Where \(n\) is the number of sides, and \(s\) is the length of a side, and \(r\) is the outer radius (the radius of a circumscribed circle), the
perimeter of a regular polygon can be calculated as follows:
One might not think of a circle as a regular polygon, but in reality, a circle is a regular polygon with an infinite number of sides. If we were to evaluate \(ν\) as the limit \(ν=\lim\limits_{n\to\infty}n\,sin\frac{π}{n}\), we would get \(ν=π\) as a result. The perimeter of a circle is then \(2νr=2πr\). Area of Regular PolygonsSince a regular polygon is composed of \(n\) isosceles triangles, each with an area of \(k=\frac{1}{2}sa\), where \(s\) is the length of one side, and \(a\) is the length of the inner radius of the polygon (the radius of an incribed circle), it follows that the polygon will have an area equal to \(n(\frac{1}{2}sa)\), where \(n\) is the number of sides; therefore, for any regular polygon, the area \(k\) can be calculated as: Also, in terms of radius \(r\): And in terms of perimeter, where \(ρ=\frac{r}{2ν}\): If we know the area and number of sides, we can determine that the length of a side is: And if we know the side length and number of sides, we can determine the inner radius \(a\) and outer radius \(r\): The area formula \(A=\frac{1}{2}ρa\), as described before can be used for any regular polygon. A regular polygon always has sides of equal length. Below are some examples: 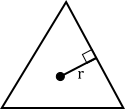
As long as all three sides of a triangle have equal length, then it is a regular polygon and has an area equal to:
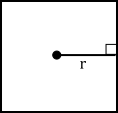
A square is the regular polygon with 4 sides:

A hexagon has six equal sides:

As stated before, a circle is a regular polygon with an infinite number of sides:

A pentagram is also a regular polygon. Remember to use the inner radius:

The same is true of a hexagram, or any similar shape with equal-length sides:

A rhombus might not look like a regular polygon, but it is:
|
||
| Geometry: Triangles |